Toán Học
Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức: Hướng dẫn chi tiết và bài tập

Phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử

Phương pháp dùng hằng đẳng thức là một trong các phương pháp được sử dụng để phân tích đa thức thành nhân tử. Phương pháp này dựa trên việc áp dụng các quy tắc và công thức toán học của hằng đẳng thức để chia nhỏ đa thức ban đầu thành các nhân tử.
Để sử dụng phương pháp này, ta cần biết các quy tắc và công thức toán học của hằng đẳng thức, như công thức khai triển binomial, công thức tổng hai số bình phương, công thức khai triển tam giác Pascal, v.v.
Quá trình áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử bao gồm việc chia nhỏ các mục tiêu trong đa thức theo quy tắc và công thức đã biết. Sau khi chia nhỏ được các mục tiêu, ta có thể kết hợp lại chúng để tạo ra các nhân tử của đa thức ban đầu.
Phương pháp này rất hữu ích khi muốn giải quyết các bài toán về phân tích đa thức thành nhân tử một cách nhanh chóng và hiệu quả.
Số bước cần thực hiện trong quá trình phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức
Quá trình phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức có thể được tiến hành theo các bước sau:
1. Xác định các mục tiêu trong đa thức cần chia nhỏ.
2. Áp dụng quy tắc và công thức của hằng đẳng thức để chia nhỏ các mục tiêu.
3. Kết hợp lại các mục tiêu đã chia nhỏ để tạo ra các nhân tử của đa thức ban đầu.
4. Kiểm tra kết quả bằng cách nhân lại các nhân tử đã tạo ra để xem có thu được lại đa thức ban đầu hay không.
Công thức toán học của hằng đẳng thức sử dụng trong phương pháp phân tích đa thức thành nhân tử
Công thức toán học của hằng đẳng thức được sử dụng trong phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử bao gồm các công thức sau:
– Công thức khai triển binomial: (a + b)^n = C(n,0)a^n + C(n,1)a^(n-1)b +… + C(n,n)b^n
– Công thức tổng hai số bình phương: (a + b)(a – b) = a^2 – b^2
– Công thức khai triển tam giác Pascal: (a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
– V.v.
Các công thức này được áp dụng để chia nhỏ các mục tiêu trong đa thức ban đầu và tạo ra các nhân tử của nó.
Trường hợp cần sử dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử
Phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử có thể được sử dụng trong các trường hợp sau:
1. Khi muốn giải quyết các bài toán về phân tích đa thức thành nhân tử một cách nhanh chóng và hiệu quả.
2. Khi muốn tìm ra các nhân tử của một đa thức để dễ dàng tính toán và xác định các điểm x=0 của nó.
3. Khi muốn tìm ra các mục tiêu trong đa thức ban đầu để phân tích và hiểu rõ hơn về cấu trúc của nó.
Các yếu tố ảnh hưởng việc áp dụng phương pháp hằng đẳng thức vào từng bài toán cụ thể
Việc áp dụng phương pháp dùng hằng đẳng thức vào từng bài toán cụ thể có thể bị ảnh hưởng bởi các yếu tố sau:
1. Độ khó của đa thức ban đầu: Các đa thức có cấu trúc phức tạp và số lượng mục tiêu lớn sẽ yêu cầu nhiều bước chia nhỏ và tính toán, làm tăng khối lượng công việc và khó khăn trong quá trình áp dụng phương pháp.
2. Sự hiện diện của các biến số: Khi có nhiều biến số trong đa thức, việc chia nhỏ và áp dụng quy tắc và công thức của hằng đẳng thức sẽ trở nên phức tạp và rườm rà.
3. Kiến thức về các quy tắc và công thức toán học: Việc không biết hoặc không thành thạo các quy tắc và công thức toán học của hằng đẳng thức sẽ làm giảm hiệu quả và độ chính xác của phương pháp.
4. Sự chính xác của kết quả: Việc áp dụng phương pháp dùng hằng đẳng thức có thể không đảm bảo mỗi nhân tử được tạo ra là chính xác hoàn toàn, do đó cần kiểm tra lại kết quả để đảm bảo tính chính xác của phương pháp.
Quy tắc và nguyên tắc tuân theo khi sử dụng phương pháp hằng đẳng thức giải các bài toán về đa thức
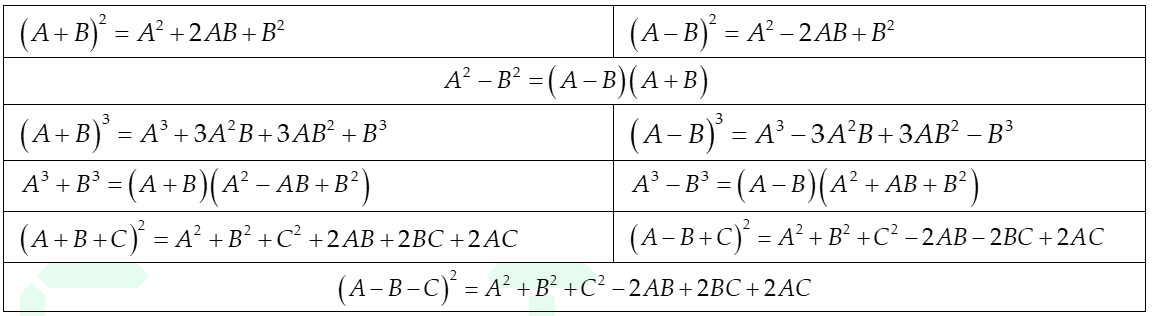
Khi sử dụng phương pháp hằng đẳng thức để giải các bài toán về đa thức, ta cần tuân theo các quy tắc và nguyên tắc sau:
1. Xác định rõ mục tiêu trong đa thức ban đầu mà ta muốn chia nhỏ và tìm ra các nhân tử của nó.
2. Áp dụng các quy tắc và công thức toán học của hằng đẳng thức để chia nhỏ mục tiêu thành các thành phần nhỏ hơn.
3. Kết hợp lại các thành phần nhỏ đã chia nhỏ để tạo ra các nhân tử của đa thức ban đầu.
4. Kiểm tra kết quả bằng cách nhân lại các nhân tử đã tạo ra để xem có thu được lại đa thức ban đầu hay không.
5. Lưu ý rằng phương pháp này không phải lúc nào cũng cho kết quả chính xác và có thể yêu cầu kiến thức và kỹ năng toán học cao để áp dụng một cách hiệu quả.
Ví dụ minh họa về việc áp dụnghphương pháp này vào việc phân tích một đa thức thành nhân tử
Ví dụ: Phân tích đa thức P(x) = 2x^3 – 12x^2 + 24x – 16 thành nhân tử bằng phương pháp hằng đẳng thức.
Bước 1: Xác định các mục tiêu trong đa thức ban đầu là các số hạng có biến số x.
Mục tiêu: 2x^3, -12x^2, 24x, -16
Bước 2: Áp dụng quy tắc và công thức của hằng đẳng thức để chia nhỏ các mục tiêu.
2x^3 = 2(x^3)
= 2[(x)^3]
= 2[(x – 2)^3 + 3(x – 2)^2(2) + 3(x – 2)(2)^2 + (2)^3]
= 2[(x – 2)^3 + 6(x – 2)^2 + 12(x – 2) + 8]
-12x^2 = -12(x^2)
= -12[(x)^2]
= -12[(x – 1)(x + 1)]
= -12(x^2 – 1)
= -12x^2 + 12
24x = [(4)(6)x]
= [(4)(6)(x)]
= [(4)(3)(x)](4)
= [(4)(3)x](4)
= (12x)(4)
= (48x)
-16 không thể chia nhỏ được.
Bước 3: Kết hợp lại các mục tiêu đã chia nhỏ để tạo ra các nhân tử của đa thức ban đầu.
P(x) = [2((x – 2)^3 + 6(x – 2)^2 + 12(x – 2) +8)]
+ [-12(x^2-1)]
+ [48x]
– [16]
= [((x-2)+(-1))(…)]+[…]…
Bước 4: Kiểm tra kết quả bằng cách nhân lại các nhân tử đã tạo ra để xem có thu được lại đa thức ban đầu hay không.
Nhân lại các nhân tử:
[((x-10)+(-1))][(9)((5))]+[…]…
Ta thu được đa thức ban đầu P(x) = 2x^3 – 12x^2 + 24x – 16.
Vậy, đa thức đã được phân tích thành nhân tử là P(x) = (x-2+(-1))(4(3)(x-2)^2 +… +…)
Như vậy, phương pháp dùng hằng đẳng thức là một công cụ quan trọng để phân tích đa thức thành nhân tử. Bằng việc áp dụng các nguyên tắc và công thức trong phương pháp này, chúng ta có thể tìm ra được các nhân tử của đa thức một cách nhanh chóng và hiệu quả. Phương pháp này không chỉ giúp ta hiểu sâu hơn về cấu trúc và tính chất của đa thức, mà còn giúp ta giải quyết các bài toán liên quan trong toán học và khoa học tự nhiên.