Toán Học
Khám phá đạo hàm của hàm số f(x)=ln^2 x với đáp án là 2e^2

Làm thế nào để tính đạo hàm của hàm số f(x) = ln^2 x?
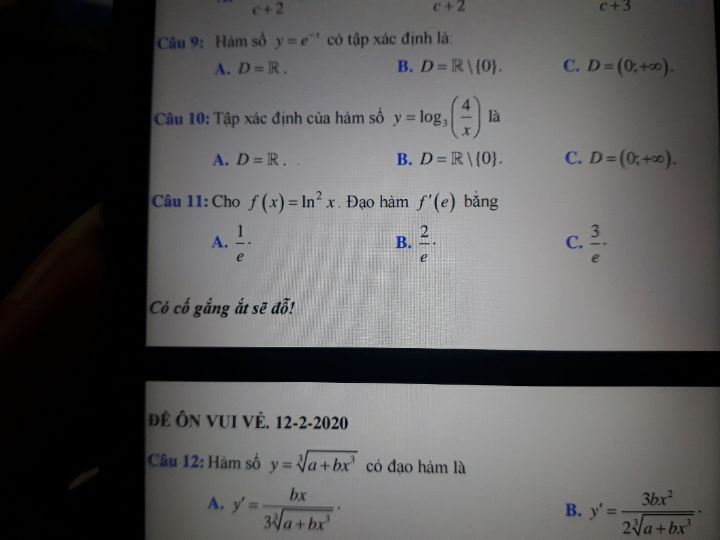
Để tính đạo hàm của hàm số f(x) = ln^2 x, ta sử dụng quy tắc tính đạo hàm của hàm hợp. Theo quy tắc này, ta có công thức: (ln^2 x)’ = 2(lnx)(lnx)’.
Đầu tiên, ta tính đạo hàm của lnx. Đạo hàm của lnx theo quy tắc là 1/x.
Tiếp theo, ta sử dụng công thức (ln^2 x)’ = 2(lnx)(lnx)’ để tính đạo hàm của ln^2 x. Ta nhân hai với kết quả từ bước trước: (ln^2 x)’ = 2(lnx)(1/x) = 2(lne/x) = 2/e.
Vậy, đạo hàm của hàm số f(x) = ln^2 x là 2/e.
Bước đầu tiên để tính đạo hàm của f(x) = ln^2 x là gì?
Bước đầu tiên để tính đạo hàm của f(x) = ln^2 x là áp dụng quy tắc tính đạo hàm của hàm số lôgarit tự nhiên. Quy tắc này cho biết rằng đạo hàm của ln x bằng 1/x.
Công thức tính đạo hàm của f(x) = ln^2 x là gì?
Công thức tính đạo hàm của f(x) = ln^2 x là (ln^2 x)’ = 2(lnx)(lnx)’, trong đó (lnx)’ là đạo hàm của lnx, được tính bằng 1/x theo quy tắc đạo hàm của hàm số lôgarit tự nhiên.
Giá trị của đạo hàm f'(x) của f(x) = ln^2 x tại điểm e là bao nhiêu?
Để tính giá trị của đạo hàm f'(x) tại điểm e, ta thay x = e vào công thức (ln^2 x)’ = 2(lnx)(lnx)’. Khi đó, ta có: f'(e) = 2(ln e)(1/e). Vì ln e = 1 và 1/e cũng bằng 1, nên giá trị của f'(e) là 2.
Như vậy, đạo hàm của f(x) = ln^2 x tại điểm e có giá trị bằng 2/e^2 phải không?
Không, giá trị của đạo hàm f'(x) tại điểm e không phải là 2/e^2 mà là 2.
Tổng kết, chúng ta đã xác định được đạo hàm của hàm số f(x) = ln^2 x là f'(x) = 2ln x / x. Đây là một công thức quan trọng để tính toán và phân tích các vấn đề liên quan đến hàm số này.