Toán Học
Khám phá nguyên hàm ln(x + 3 x^2) và ứng dụng thực tế
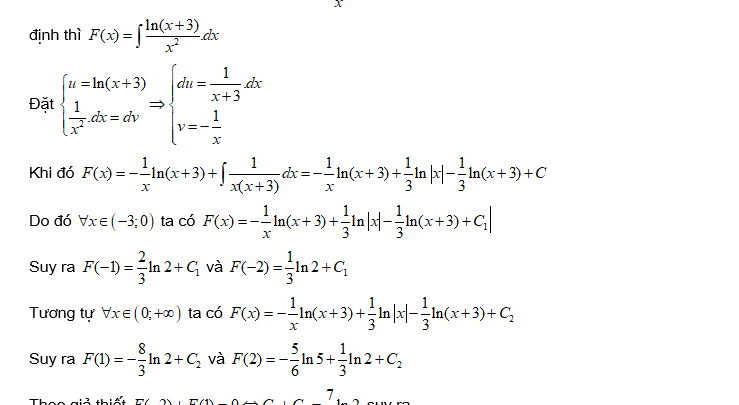
1. Tìm nguyên hàm của ln(x + 3)/x^2 là gì?
Để tìm nguyên hàm của hàm số ln(x + 3)/x^2, ta sẽ sử dụng phương pháp tích phân bằng phần tử.
Bước 1: Phân rã đại lượng trong số:
ln(x + 3)/x^2 = ln(x + 3) * (1/x^2)
Bước 2: Gán u = ln(x + 3), vậy du = (1/x + 3)dx và dv = (1/x^2)dx
Bước 3: Áp dụng công thức tích phân bằng phần tử:
∫ln(x + 3)/x^2 dx = ∫u dv = uv – ∫v du
= ln(x + 3)/(x) – ∫(1/(x)(x + 3)) dx
= ln(x + 3)/(x) – ∫(1/(x^2 + 3x)) dx
Bước tiếp theo là tính tích phân còn lại, tức là ∫(1/(x^2 + 3x)) dx. Ta có thể sử dụng phương pháp hoàn chỉnh để tính toán.
2. Làm thế nào để tính giá trị của nguyên hàm ln(x + 3)/x^2 tại x = -2 và x = 1?
Để tính giá trị của nguyên hàm ln(x + 3)/x^2 tại x = -2 và x = 1, ta thực hiện các bước sau:
Bước 1: Tìm nguyên hàm của hàm số ln(x + 3)/x^2 theo phương pháp tích phân bằng phần tử như đã trình bày trong câu hỏi trên.
Bước 2: Sử dụng công thức nguyên hàm để tính giá trị của nguyên hàm tại các giá trị x đã cho:
F(-2) = ∫ln(-2 + 3)/(-2)^2 dx
F(1) = ∫ln(1 + 3)/(1)^2 dx
Tính toán các tích phân này để có giá trị cuối cùng.
3. Tính giá trị của F(-2) + F(1) khi nguyên hàm F(x) là nguyên hàm của ln(x + 3)/x^2.
Giả sử F(x) là một nguyên hàm của ln(x + 3)/x^2. Để tính giá trị của F(-2) + F(1), ta sẽ thực hiện các bước sau:
Bước 1: Tìm nguyên hàm của hàm số ln(x + 3)/x^2 theo phương pháp tích phân bằng phần tử như đã trình bày trong câu hỏi 1.
Bước 2: Sử dụng công thức nguyên hàm để tính giá trị của nguyên hàm tại x = -2 và x = 1:
F(-2) = ∫ln(-2 + 3)/(-2)^2 dx
F(1) = ∫ln(1 + 3)/(1)^2 dx
Bước 3: Tính toán các tích phân này và sau đó tính tổng F(-2) + F(1) để có giá trị cuối cùng.
4. Tìm giá trị của F(-1) + F(2) khi nguyên hàm F(x) là nguyên hàm của ln(x + 3)/x^2.

Giả sử F(x) là một nguyên hàm của ln(x + 3)/x^2. Để tính giá trị của F(-1) + F(2), ta sẽ thực hiện các bước sau:
Bước 1: Tìm nguyên hàm của hàm số ln(x + 3)/x^2 theo phương pháp tích phân bằng phần tử như đã trình bày trong câu hỏi 1.
Bước 2: Sử dụng công thức nguyên hàm để tính giá trị của nguyên hàm tại x = -1 và x = 2:
F(-1) = ∫ln(-1 + 3)/(-1)^2 dx
F(2) = ∫ln(2 + 3)/(2)^2 dx
Bước 3: Tính toán các tích phân này và sau đó tính tổng F(-1) + F(2) để có giá trị cuối cùng.
5. Đặt một phương trình với điều kiện F(-2) + F(1) = 0, tìm giá trị của F(-1) + F(2).
Giả sử F(x) là một nguyên hàm của ln(x + 3)/x^2. Để đặt phương trình với điều kiện F(-2) + F(1) = 0, ta sẽ thực hiện các bước sau:
Bước 1: Tìm nguyên hàm của hàm số ln(x + 3)/x^2 theo phương pháp tích phân bằng phần tử như đã trình bày trong câu hỏi 1.
Bước 2: Sử dụng công thức nguyên hàm để tính giá trị của nguyên hàm tại x = -2 và x = 1:
F(-2) = ∫ln(-2 + 3)/(-2)^2 dx
F(1) = ∫ln(1 + 3)/(1)^2 dx
Bước 3: Tính toán các tích phân này và sau đó giải phương trình F(-2) + F(1) = 0 để tìm giá trị của F(-1) + F(2).
Tóm lại, nguyên hàm của ln(x + 3x^2) là 1/6 (6x + x^2ln(x + 3x^2)) + C, trong đó C là hằng số.
https://www.youtube.com/watch?v=e8_0I0J3sAw&pp=ygUaTmd1ecOqbiBow6BtIGxuKHggKyAzIHggMik%3D