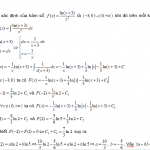Toán Học
Tìm hiểu về nguyên hàm ln(x+3): Định nghĩa, công thức và ứng dụng

1. Công thức nguyên hàm của hàm ln(x+3) là gì?
Công thức nguyên hàm của hàm ln(x+3) được biểu diễn bởi F(x) = ∫ln(x+3)dx. Đây là công thức để tính giá trị của nguyên hàm của hàm ln(x+3). Trong đó, ln(x+3) là một hàm logarithm tự nhiên với cơ số e và x+3 là biến số trong hàm logarithm.
Để tính giá trị của nguyên hàm ln(x+3), ta sử dụng kỹ thuật tích phân. Kỹ thuật này giúp chúng ta tìm ra một hàm F(x) sao cho đạo hàm của F(x) là chính xác bằng với hàm gốc, tức là F'(x) = ln(x+3).
Để áp dụng công thức này, ta có thể sử dụng quy tắc tích phân và quy tắc đạo hàm để tìm được nguyên hàm cụ thể của ln(x+3).
2. Làm thế nào để tính được giá trị của nguyên hàm ln(x+3)?
Để tính giá trị của nguyên hàm ln(x+3), ta có thể sử dụng các phương pháp tích phân khác nhau như:
– Sử dụng quy tắc đặc biệt: Ta có thể sử dụng quy tắc đặc biệt cho hàm ln(x+3) và tính nguyên hàm theo công thức cụ thể.
– Áp dụng phép đổi biến số: Đôi khi, chúng ta có thể áp dụng phép đổi biến số để đơn giản hóa tính toán. Ví dụ, ta có thể đặt u = x+3 và tính nguyên hàm của ln(u) theo u, sau đó chuyển về biến x bằng cách giải phương trình u = x+3.
Ngoài ra, có thể sử dụng các công cụ tính toán hoặc phần mềm máy tính để tính giá trị chính xác của nguyên hàm ln(x+3). Công cụ này sẽ tự động áp dụng các quy tắc và kỹ thuật tích phân để tính toán kết quả một cách chính xác và nhanh chóng.
3. Tại sao ta cần tính nguyên hàm của hàm ln(x+3)?

Tính nguyên hàm của hàm ln(x+3) được sử dụng trong nhiều lĩnh vực khác nhau. Một trong những ứng dụng quan trọng của nguyên hàm là tính diện tích dưới đồ thị của hàm số. Khi ta tính giá trị nguyên hàm, chúng ta có thể biết được diện tích được bao phủ bởi đồ thị hàm ln(x+3) trên một khoảng xác định.
Ngoài ra, nguyên hàm của ln(x+3) cũng có ứng dụng trong các vấn đề liên quan đến tốc độ thay đổi và tăng trưởng. Công thức này cho phép chúng ta tính toán sự thay đổi tỷ lệ của một biến số theo một biến số khác được biểu diễn bởi hàm ln(x+3).
Tính nguyên hàm cũng cần thiết để giải các bài toán tích phân trong các lĩnh vực như toán cao cấp, vật lý, kinh tế và xác suất.
4. Liệu có phương pháp nào khác để tính nguyên hàm của hàm ln(x+3) không?
Có nhiều phương pháp khác nhau để tính nguyên hàm của hàm ln(x+3). Một trong những phương pháp tiếp cận là sử dụng phương pháp tích phân riêng biệt, trong đó ta cần tìm một hàm F(x) sao cho đạo hàm của F(x) là chính xác bằng với hàm gốc ln(x+3).
Có thể áp dụng quy tắc đặc biệt cho hàm ln(x+3) và tính nguyên hàm theo công thức cụ thể. Đồng thời, ta cũng có thể sử dụng các công cụ tính toán hoặc phần mềm máy tính để tính giá trị chính xác của nguyên hàm.
5. Nguyên hàm ln(x+3) có ứng dụng trong lĩnh vực nào?
Nguyên hàm ln(x+3) được áp dụng trong nhiều lĩnh vực khác nhau như:
– Toán cao cấp: Trong toán cao cấp, nguyên hàm của ln(x+3) được sử dụng để tính diện tích dưới đồ thị và giải các bài toán liên quan đến tốc độ thay đổi.
– Vật lý: Nguyên hàm này có ứng dụng trong vật lý để tính toán các vấn đề liên quan đến tăng trưởng, tốc độ và gia tốc.
– Kinh tế: Trong kinh tế, nguyên hàm của ln(x+3) được sử dụng trong các mô hình tài chính để tính toán tỷ suất thay đổi và lợi nhuận.
– Xác suất và thống kê: Nguyên hàm này có ứng dụng trong xác suất và thống kê để tính toán phân bố xác suất và ước lượng tham số.
Trên thực tế, nguyên hàm ln(x+3) cũng có nhiều ứng dụng khác, tuỳ thuộc vào lĩnh vực và bối cảnh sử dụng của nó.
Tổng kết, nguyên hàm của hàm số ln(x+3) là Ln|x+3| + C, trong đó Ln là logarit tự nhiên và C là hằng số.
https://www.youtube.com/watch?v=Wd81h1R1o08&pp=ygUUbmd1ecOqbiBow6BtIGxuKHgrMyk%3D